链表链表,顾名思义,指的是由链子组成的数据表。
与我们常见的数组,栈,队列等顺序数据结构不同,链表的存储是不连续的。这时候可能有聪明的小朋友就要问了:“不连续存放数据怎么对数据操作啊?”别忘了,我们有链子啊。打个比方,你带你家狗出去溜弯,你也没抱着狗出门不是么?相反,你用一根狗链子牵着,就算你蒙着眼睛你也能知道你家又在哪儿。这时候假设你有超多条狗,你要带他们一起出门,但是你只愿意牵着一根狗链子,你就可以把狗与狗之间通过链子连在一起,这样你只需要牵着离你最近的一条狗也就可以得到你所有狗的位置。
(什么?你养的是猫?)
(滚。)
通常情况下,链表有多种形式,最为常见也是最为便捷的便是一种双向非循环式的链表,他大约长这样。
每一个节点长这样,并用一个结构体去存放
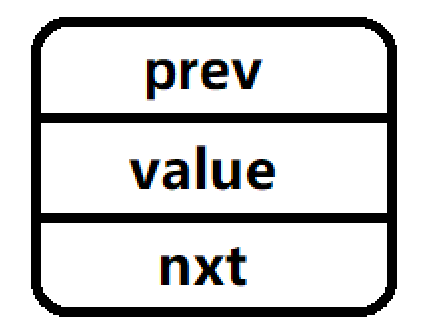
struct node
{
node *prev;
int value;
node *nxt;
};
其中prev表示其前驱节点的地址,nxt表示后驱节点的地址,value则表示当前节点的值。
将多个这样的节点连接起来,就得到了链表

这里我们以一条题目去更好的理解链表的使用
而对于链表的增添操作就更加简单,我们只需要断开原先的连接,添加上新的连接即可。




我们这里就用一个简单的题目,去方便大家理解链表操作的便捷性与增减数据时的高效性。
题目描述
一个学校里老师要将班上\(N\)个同学排成一列,同学被编号为\(1∼N\),他采取如下的方法:
先将\(1\)号同学安排进队列,这时队列中只有他一个人;
\(2−N\)号同学依次入列,编号为i的同学入列方式为:老师指定编号为i的同学站在编号为\(1~(i−1)\)中某位同学(即之前已经入列的同学)的左边或右边;
从队列中去掉\(M (M<N)\)个同学,其他同学位置顺序不变。
在所有同学按照上述方法队列排列完毕后,老师想知道从左到右所有同学的编号。
输入格式
第\(1\)行为一个正整数\(N\),表示了有\(N\)个同学。
第\(2−N\)行,第ii行包含两个整数\(k,p\),其中\(k\)为小于\(i\)的正整数,\(p\)为\(0\)或者\(1\)。若\(p\)为\(0\),则表示将\(i\)号同学插入到\(k\)号同学的左边,\(p\)为\(1\)则表示插入到右边。
第\(N+1\)行为一个正整数\(M\),表示去掉的同学数目。
接下来\(M\)行,每行一个正整数\(x\),表示将\(x\)号同学从队列中移去,如果\(x\)号同学已经不在队列中则忽略这一条指令。
输出格式
\(1\)行,包含最多\(N\)个空格隔开的正整数,表示了队列从左到右所有同学的编号,行末换行且无空格。
本题中的队列增添删去次数超过\(1×10^5\)次,使用一般的数组去进行操作根本不可能,而这正是链表所擅长的地方,对于节点的增添与删除只涉及到本身已经前驱后驱(如果存在)节点中的指针值,所需的时间几乎可以忽略不计。
再加上本题当中数据值不重复,我们就可以利用一个“桶”去建立所有节点的地址索引并实时更新,这就使得我们的操作效率得到大大提高,在1s内完成 \(1×10^5\)次 操作成为可能。
先上代码,大家可以通过注释去理解linkedlist_add()与linkedlist_erase()这两个最常用的函数
/*
* @Author: Gehrychiang
* @LastEditTime: 2020-03-31 15:42:01
* @Website: www.yilantingfeng.site
* @E-mail: gehrychiang@aliyun.com
*/
#pragma GCC optimize(2)
#include <bits/stdc++.h>
using namespace std;
struct node
{
node *prev;
int value;
node *nxt;
};
node *ptr[100005]; //存放节点地址,便于检索
node *curhead; //为了便于输出所以用一个不断更新的头结点
void linkedlist_add(int value, node *pos, int opr) //需要插入的值以及(前/后驱)位置
{
node *addon = (node *)malloc(sizeof(node)); //申请空间存放节点
(*addon).value = value;
ptr[value] = addon;
(*addon).prev = NULL;
(*addon).nxt = NULL;
if (opr == 1) //向右
{
(*addon).prev = pos;
if ((*pos).nxt != NULL) //非tail节点添加
{
(*addon).nxt = (*pos).nxt;
(*(*addon).nxt).prev = addon;
}
(*pos).nxt = addon;
}
else
{
(*addon).nxt = pos;
if ((*pos).prev != NULL) //非tail节点添加
{
(*addon).prev = (*pos).prev;
(*(*addon).prev).nxt = addon;
}
else //tail节点需要更新curhead值
{
curhead = addon;
}
(*pos).prev = addon;
}
}
void linkedlist_erase(node *pos) //删除pos处的的节点
{
if ((*pos).nxt == NULL) //删除tail节点
{
(*(*pos).prev).nxt = NULL;
}
else if ((*pos).prev == NULL) //删除head节点
{
(*(*pos).nxt).prev = NULL;
curhead = (*pos).nxt; //更新curhead值
}
else //非首尾节点
{
(*(*pos).prev).nxt = (*pos).nxt; //重建连接
(*(*pos).nxt).prev = (*pos).prev;
}
ptr[(*pos).value] = NULL; //重置索引
}
int main()
{
//freopen("","r",stdin);
//freopen("","w",stdout);
node head;
head.value = 1;
head.nxt = NULL;
head.prev = NULL;
ptr[head.value] = &head;
curhead = &head;
int n;
cin >> n;
for (int i = 2; i <= n; i++)
{
int k, p;
cin >> k >> p;
linkedlist_add(i, ptr[k], p);
}
int t;
cin >> t;
while (t--)
{
int tmp;
cin >> tmp;
if (ptr[tmp] != NULL) //存在此节点
{
linkedlist_erase(ptr[tmp]); //删除
}
}
//最后按照从头节点向尾结点递归输出值即可
while (1)
{
cout << (*curhead).value << " ";
if ((*curhead).nxt != NULL)
{
curhead = (*curhead).nxt;
}
else
{
break;//到头了
}
}
//fclose(stdin);
//fclose(stdout);
return 0;
}

