我们之前已经大约说到了关于多重背包的问题,是针对每一个物体而言为深度维度去进行的研究,现在让我们将问题研究的尺度从深度向广度延展,如果在背包的物品当中存在彼此之间的相关性我们应该怎么去处理呢。这就是我们在这篇文章中所要研究的话题——物品之间存在前置依赖关系的背包问题。
前置知识:01背包(了解恰好背包的实现逻辑),分组背包。
这个问题的来源是NOIP 2006 提高组 金明的预算方案
我们这里简单的将问题压缩抽象一下,就是你有一个容量为\(N\)的背包,需要往其中放入最多的物品,但是这一次的物品之间存在依赖关系,即有的物品为“主件”,可以单独购买,而有的物品为“附件”,每一个附件都有唯一的对应“主件”,必须要在购买主件的基础上才能购买相应的附件。
与普通01背包的唯一不同其实就是在于该问题当中存在组的概念。
以题目所给的样例为例
1000 5 800 2 0 400 5 1 300 5 1 400 3 0 500 2 0
第一个物品为主件(序号是0),第二个第三个物品则为第一个物品的附件,第四个第五个物品又为主件。
让我们画个图出来
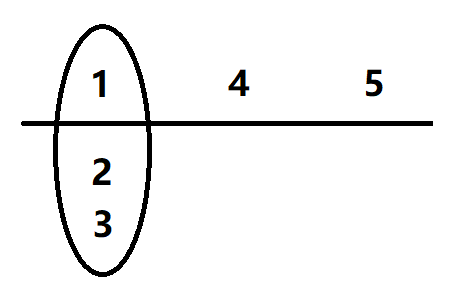
我们处理这类题目其实是需要进行一个分组dp的操作,因为显然物品之间存在依赖关系但是这样的一种依赖关系并不会脱离于其主件而存在,而我们需要去做的则是在组内先进行一次dp,再将本组的结果与其他各个组合并,便是我们去做这一题的一个思路。
需要注意的是,这一题虽然思路还算比较明朗,但是编码的过程存在很多细节性的问题,我来大致地说一说。
首先是一个结果的存放问题,需要开一个dp[]用来临时存放每一组内进行运算的结果。而这个结果需要在一组结束之后转存到一个V[][]和P[][]数组当中去,用来记录每一个主件所构成的主附件组内的价格和价值的分配情况,最后分组dp的来源也就是这个V[][]和P[][]数组。
其次是一个恰好背包的概念。刚才已经说了V[][]存储的是价格分配情况,P[][]是价值分配情况,价格和价值的关系在我们平时一般做dp问题的时候通常是给予冗余的,也就是每一个最优解的实际使用的价格是小于等于我在这个最优解情况下所能使用的解的,但这一题因为我们后期是要进行一个分组dp合并的一个操作,其实是将每一组的dp结果视为一个个物品加以合并,这也就意味着冗余的钱并不会得到利用而只会浪费掉,不能真实地反映我的终了情况。故此,我们在每一组内进行01背包的时候其实是需要去进行一个“恰好背包”的处理,也就是每一个最优解是把钱花完的(背包装满的)。处理恰好背包的操作我们在前面的文章中已经说得很详细了。
先提供代码,方便大家更好的去理解,注释也已经写的非常详细了,最后再进行总结
/*
* @Author: Gehrychiang
* @LastEditTime: 2020-04-06 00:29:25
* @Website: www.yilantingfeng.site
* @E-mail: gehrychiang@aliyun.com
*/
//#pragma GCC optimize(2)
#include <bits/stdc++.h>
using namespace std;
struct node
{
int v; //价格
int p; //重要度
int q; //主附件
};
node a[105]; //存储物品
node cnc[105][105]; //存储主附件相关性
int n; //钱
int m; //物品
int dp[320055]; //dp行
int t[105]; //存储每一个主件的附件数
int cnt[105]; //存储每一个主件的合法分配
int V[105][10]; //存储分组dp后的每一组价格情况(需要注意是其中每一组的价格都是主件价格+x)
int P[105][10]; //存储分组dp后的每一组重要度情况
int main()
{
//freopen("","r",stdin);
//freopen("","w",stdout);
cin >> n >> m;
for (int i = 1; i <= m; i++)
{
cin >> a[i].v >> a[i].p >> a[i].q;
if (a[i].q != 0) //此为附件,需要更新其主件的相关性
{
t[a[i].q]++; //更新个数
cnc[a[i].q][t[a[i].q]] = a[i]; //更新节点
}
}
for (int i = 1; i <= m; i++) //对每一组进行01背包
{
if (a[i].q == 0) //遇到一个主件,开始进行该组内的dp
{
memset(dp, -1, sizeof(dp)); //需要注意是恰好的背包安排(因为我们需要将下标占用与实际占用一一对应)
dp[0] = 0;
for (int j = 1; j <= t[i]; j++) //有t[i]个附件
{
for (int k = n - a[i].v; k >= cnc[i][j].v; k--) //该组所能花费的最多金额就是总钱数-主件价格(n - a[i].v),而(如果买的话)下限就是当前附件的价格
{
if (dp[k - cnc[i][j].v] != -1) //必须要保证我是从价格为0开始逐层累加的dp,以保证恰好背包
dp[k] = max(dp[k - cnc[i][j].v] + cnc[i][j].v * cnc[i][j].p, dp[k]); //01背包
}
}
for (int j = 0; j <= n - a[i].v; j++) //组结果转存,该组所能花费的最多金额就是总钱数-主件价格
{
if (dp[j] != -1) //每有一个非-1的解,这就是一个合法解
{
cnt[i]++; //记录当前主件的合法解个数
V[i][cnt[i]] = a[i].v + j; //总价格为dp结果的价格+主件价格(因为我们在dp的过程当中实质上是没有参与主件的,或者说价格为0的时候就是仅购买主件的解)
P[i][cnt[i]] = dp[j] + a[i].v * a[i].p; //总价值为dp结果的价格+主件价值
}
}
}
}
//至此已经划分完成了每一组的情况
memset(dp, 0, sizeof(dp));
for (int i = 1; i <= m; i++) //每一个物品
{
if (a[i].q == 0) //(其实只有主件起到了效果)
{
for (int j = n; j >= 0; j--) //金钱,01背包逆序求解
{
for (int k = 1; k <= cnt[i]; k++) //针对每一个物品
{
if (j >= V[i][k])
dp[j] = max(dp[j], dp[j - V[i][k]] + P[i][k]);
}
}
}
}
cout << dp[n];
//fclose(stdin);
//fclose(stdout);
return 0;
}
这一题的关键其实就在于对于分组与依赖性的理解,只要能够处理好二者之间的关系,更为复杂的依赖关系也可以通过类似子类dp的方式去进行问题的拆分并解决。
这里安利一道好题Oak的预算方案,是原先题目的数据加强版,读者可以自行完成这一道题目以巩固对存在依赖关系的背包问你题的理解
最后我想说的是上面的代码是为了便于理解,更优的解法如下(其实主要是在空间上起到了优化,不用开那么多转存数组了,但是我相信读者们其实在看上面代码的时候也已经发现了很多内容其实并不必要,可以进行优化和整合)。

