本篇将介绍在各类算法竞赛中应用广泛,也是最为基础的一种素数筛法,欧拉筛,他的本质是Eratosthenes筛的优化
在介绍欧拉筛之前,我们不妨先整体感悟一点就是素数的存在虽然是无序 的 (至少目前并没有有力的证明素数的分布存在一定规律,而这就涉及到有关黎曼猜想的推论,我们暂且不谈),但却是有迹可循的,怎么有迹可循法呢?
那是因为非素数是可以很容易判定出来的,也就是一个著名的定理
著名的古希腊数学家欧几里得发现了这点,并将其记录在其著名的《原本》当中,后人将其命名为算术基本定理。
定理如下
每一个大于\(1\)的正整数均可分解为有限个素数的积,如果不计素因数在乘积中的次序,则分解方式是唯一的。将\(n\)的素因数分解中相同的素因子收集到一起,可只每个大于\(1\)的正整数\(n\)可唯一地写成
\( n = p^{a_1}_1 p^{a_2}_2 p^{a_3}_3 . . . . . . p^{a_k}_k \)
其中, \(p_1\) , \(p_2\) , \(p_3\) , . . . , \(p_k\) ,是互不相同的素数,而\(a_1\),\(a_2\),\(a_3\),. . .,\(a_k\) 是正整数
上面的分解式称为\(n\)的标准分解。
按数学家们的话来说,这个标准分解式给我们研究数的性质带来了极大的便利,因为它将整数的问题都归结到了素数上,而素数非常好的性质就是他没什么性质,具有高度的纯粹性。
废话少说,那么这样的唯一分解定理给我们筛取素数带来了什么便利呢?
我们可以这么想,如果这个数不是素数,那么他就有这样的一个性质
若\(X\)不是素数,则\(X\)必存在两个及以上的素数因子,反过来说,也就是说我们将任一素数\(P\)以自身为单位进行扩增,那么所得到的一系列数必然都不是素数。
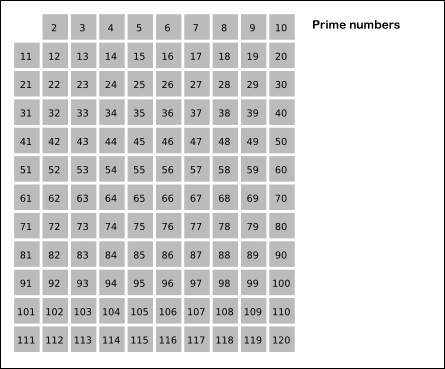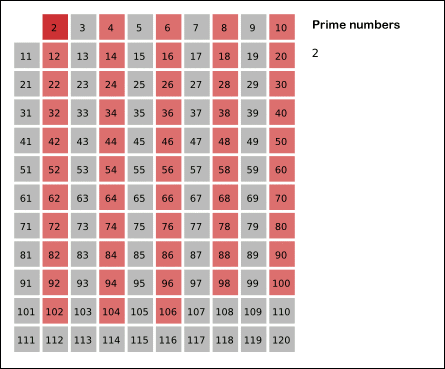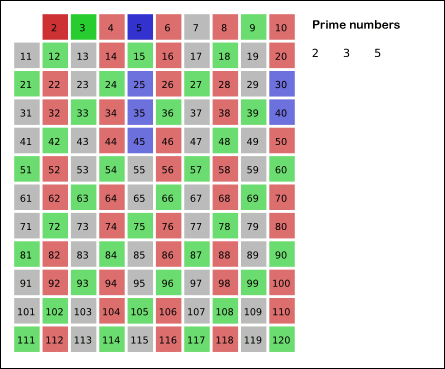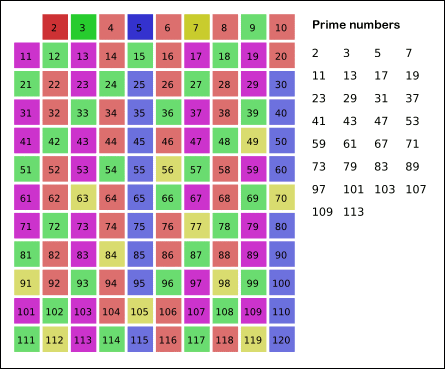
而这也就构成了我们编写算法的理论基础。
利用一个Prime数组去保存各个素数,再利用一个NotPrime数组去记录一个数是不是素数便能够在向后遍历的过程中以O(n)的时间复杂度计算出一个素数表
如果读者有兴趣更可以点此详细阅读线性筛的发现者所著论文,去更加准确地了解原理与严格的线性时间复杂度证明
以下给出模板代码
/*
* @Author: Gehrychiang
* @Date: 2019-11-26 15:37:33
* @Website: www.yilantingfeng.site
* @E-mail: gehrychiang@aliyun.com
*/
#include <bits/stdc++.h>
using namespace std;
const int MaxN = 1e6 + 5;
int prime[MaxN];
bool notprime[MaxN];
long long prisit = 1;//记录当前素数的位置(个数)
void primefilter()
{
prime[0] = 1;
notprime[0] = true;
notprime[1] = true;
for (long i = 2; i < MaxN; i++)
{
if (!notprime[i]) //如果当前值没有被非素数的判定填充
{
prime[prisit++] = i; //当前值就是素数
}
for (long long j = 1; j < prisit && i * prime[j] < MaxN; j++) //开始向后遍历,将素数的倍数全部标记为非素数
{
notprime[i * prime[j]] = true;
if (!(i % prime[j]))
{
break;
}
}
}
}
int main()
{
primefilter();
return 0;
}

