以“【模板】单源最短路径(弱化版)”为例
最短路径是图论当中的重点内容之一
这里我们借由洛谷上的一条模板题来理解一下什么是SPFA
首先明确,SPFA并不是一个算法的名字,这只是一个中国老师在1996年在Bellman–Ford算法基础上利用队列机制所改进的一个算法,可是比较尴尬的是他的证明被证明是错误的,并且同样的内容早在1959年已经得到了Moore · Edward F. 的证明。
首先看SPFA的名字(Shortest Path Faster Algorithm)貌似很厉害的样子,不过事实是SPFA面对随机性的数据依然是得心应手的(码量小啊),他还能处理带有负权边的问题,相较其他算法能够更加简单地判断负环。而这些是Dijkstra算法所不能的,但是在正权图中,最优的算法依然建议Dijkstra算法,理由请参见下文。
我们继续说SPFA
对SPFA的一个很直观的理解就是由无权图的BFS转化而来。在无权图中,BFS首先到达的顶点所经历的路径一定是最短路(也就是经过的最少顶点数),所以此时利用数组记录节点访问可以使每个顶点只进队一次,但在带权图中,最先到达的顶点所计算出来的路径不一定是最短路。一个解决方法是放弃数组,此时所需时间自然就是指数级的,所以我们不能放弃数组,而是在处理一个已经在队列中且当前所得的路径比原来更好的顶点时,直接更新最优解。
我们可以利用图像来演示这个过程。
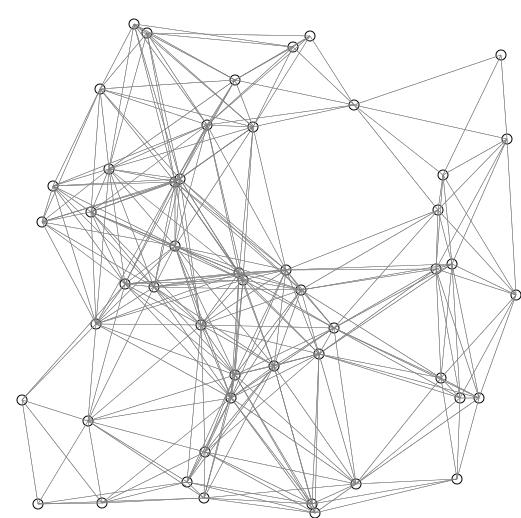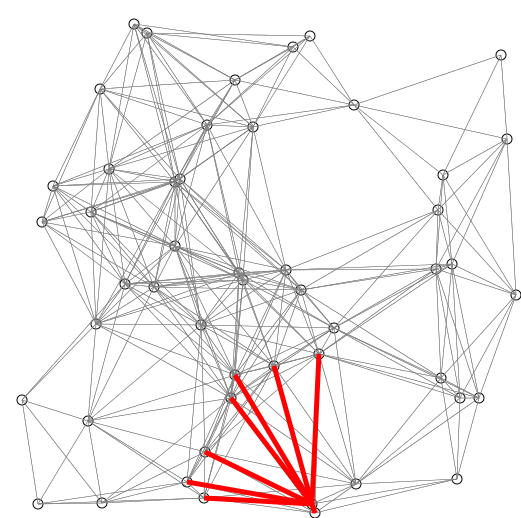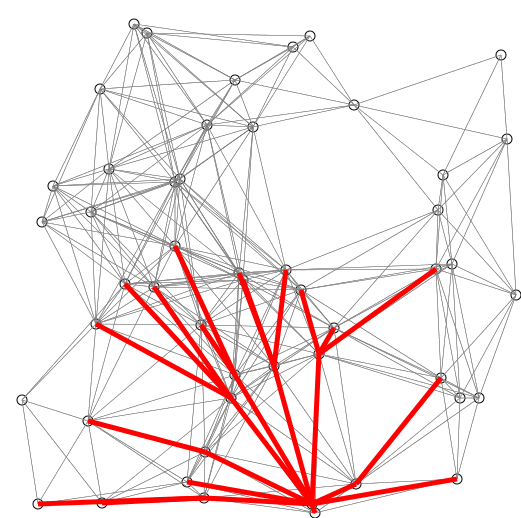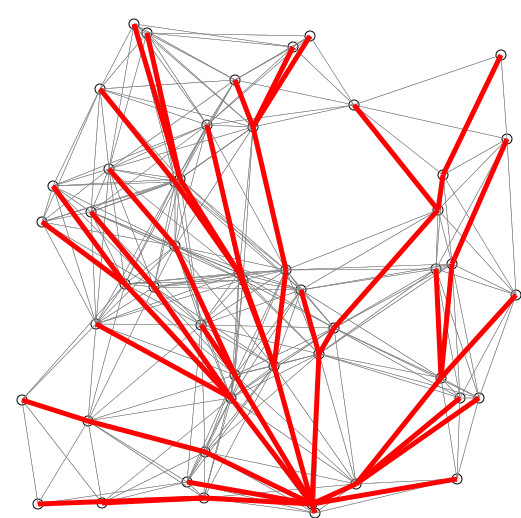
SPFA还有两个可以优化的环节(留坑)
模板代码如下
/*
* @Author: Gehrychiang
* @Date: 2020-02-11 22:48:23
* @Website: www.yilantingfeng.site
* @E-mail: gehrychiang@aliyun.com
*/
#include <bits/stdc++.h>
using namespace std;
const int INF = 1e6;
struct edge
{
int from, to, w;
edge(int a, int b, int c) { from = a, to = b, w = c; }
};
vector<edge> e[105]; //e[i]存储第i个节点连接的所有边
int n; //总节点数
int m; //总路径数
int pre[105]; //在已知最短路径上pre[a]=b,节点a的前一个节点是b
void spfa(int dept, int dest) //起点
{
int dis[105];
bool inq[105]; //判断是否在队列当中
for (int i = 1; i <= n; i++)
{
dis[i] = INF; //将节点距离置为无穷,便于之后缩小
inq[i] = false; //所以节点均不在队列中
}
int Neg[105]; //记录每个节点进入队列的次数,用来判断负环
memset(Neg, 0, sizeof(Neg)); //初始化
Neg[dept] = 1; //起点进队列第一次
dis[dept] = 0; //细节判断,起点到自己的距离为0
queue<int> q;
q.push(dept); //qidian jingru duilie
inq[dept] = true;
while (!q.empty())
{
int u = q.front();
q.pop();
inq[u] = false;
for (int i = 0; i < e[u].size(); i++) //检查u中的所有元素也就是u的所有邻居
{ //第i个邻居
int v = e[u][i].to; //从u到v
int w = e[u][i].w;
if (dis[u] + w < dis[v]) //也就是经由u到v比从其他道路到v更近
{
dis[v] = dis[u] + w; //更新距离
pre[v] = u; //更新路径,到v应该选择u
if (!inq[v]) //此时我更新了v的状态而如果v不在更新队列当中的话需要把v放进队列
{
q.push(v);
inq[v] = true;
Neg[v]++; //v进队的次数+1
if (Neg[v] > n)
{
return; //此时出现负环。无最短路
}
}
}
}
}
cout << dis[dest] << endl;
return;
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int dept, dest;//起点与终点
cin >> n >> m;
for (int i = 1; i <= n; i++) //初始化
{
e[i].clear();
}
for (int i = 0; i < m; i++)
{
int a, b, c;
cin >> a >> b >> c;
e[a].push_back({a, b, c});//双向路特别注意!
e[b].push_back({b, a, c});
}
spfa(dest, dept);
return 0;
}
最后再来说说为什么SPFA已经死了。
因为其本身的最坏复杂度达到了\(O(VE)\)并且在构造的数据下非常容易达到这个时间复杂度
以下内容来自POJ
Furthermore, it is very easy to construct a data to defeat this algorithm.
Suppose you want the shortest path from vertex \(1\) to vertex \(n\),
then we can add edge \((i, i + 1)\) with a small random weight for \(1 <= i < n\) (thus the shortest path should be \(1-2-…-n\)),
and randomly add \(4n\) other heavy edges. For this case, the so-called SPFA algorithm will be very slow.
(1) SPFA is just a variation of Bellman-Ford, and SPFA is not its real name.
(2) It works well on random sparse graph, but programming contest should consider the worst case.
(3) Anyway, it is much faster than the original Bellman-Ford,
so it will be very helpful if we want to find the shortest path in graphs containing negative weight edges,such as min cost flow problem.
然而与之相比的是djikstra算法虽然没有办法处理负权边问题但是其最坏时间复杂度提升到了\(O(V^2)\),如果使用二分堆优化的话时间复杂度可以提升到 \(O((E + V) log V)\),如果使用斐波那契堆优化的话可以达到 \(O(E + V log V)\)而这些都远比所谓的SPFA更有优势

