并查集——并查集的优化

查询优化

路径压缩

很显然，我对我的爸爸或者爷爷是谁并不在乎，我只在乎我的祖先是谁。

根据这样的思路，路径压缩的并查集就诞生了

int find(int x)
{
    if (x != fa[x])          // x不是自身的父亲，即x不是该集合的祖先
        fa[x] = find(fa[x]); // 查找x的祖先直到找到代表,并且将路径压缩
    return fa[x];
}

按秩（高度）合并

树的高度过高会导致在查询时进行过多的函数递归调用，造成无谓的时间浪费，利用待合并子树的高度差去优化合并的操作可以更好地减少查询时的时间复杂度

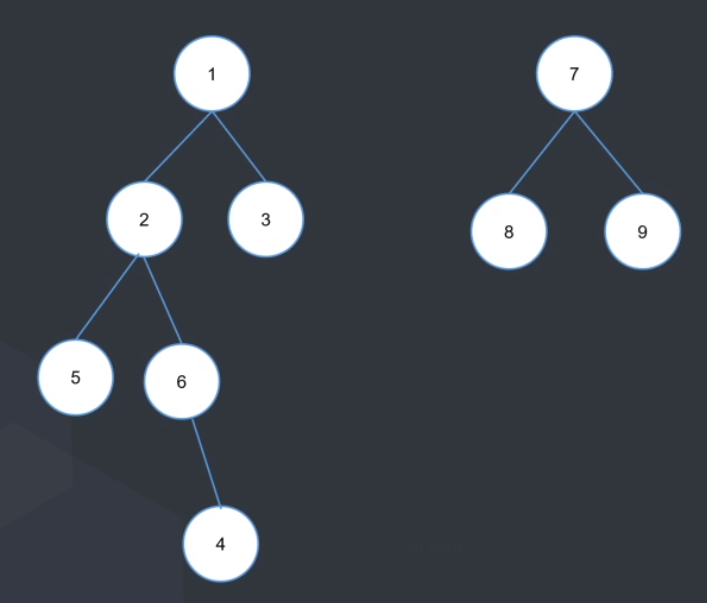
上图中，显然将右子树合并到左子树（左子树的祖先作为合并后的祖先）更优

时间复杂度

在只使用路径压缩算法或按秩合并的情况下，最坏情况下的复杂度为\(O(mlogn)\)

在同时运用的情况下，最坏时间复杂度为\(O(α(n)\)，其中\(α(n) \) 为阿克曼函数的反函数，一般情况下可以理解为常数。也就是说在同时运用的情况下，单次对并查集的操作可以优化到常数级